공학을 위한 수학 40년의 탐험

필자가 중고등학교 때 가장 좋아했던 과목이 수학이었다. 그런 배경으로 이과를 선택하고 나중에 공대로 진학하게 된다. 중학교 때는 직각 삼각형 해석에 필요한 ‘피타고라스 정리’를 증명한다고 방학 때 끙끙했던 기억도 난다. 고등학교 때는 수학책으로 ‘수학의 정석’과 ‘해법 수학’ 문제를 풀면서 좋아했다. 특히 수업 중간의 쉬는 시간이면 어려운 문제 1개씩 풀면서 10분을 지내기도 했다.

대학 입학 시험에는 본고사 수학 시험을 치렀다. 필자의 기억에 8개의 문제가 나왔는데 1개 문제를 손 대지 못하고 답을 구하지 못했다. 나중에 대학을 들어가고, 전공을 하면서 보니 아주 간단한 문제였는데, 고등학생에게는 조금 어려운 방법으로 풀어야 한다.

그 문제는 f(x)= sin(x)+sin(2x)+sin(3x)+…. +sin(nx) 의 삼각함수 수열의 합을 구하는 문제였다. 그냥 삼각함수 합의 공식으로 풀려면 불가능한데, 복소수를 이용한 삼각함수의 정의를 이용하면 쉽게 풀 수 있다. 삼각함수는 지수 함수를 복소수로 표현하면 되고, 복소수 지수함수 수열의 덧셈은 간단한 수식으로 구해진다. 이 문제를 풀려면, 삼각함수, 복소수, 수열을 개념을 통합해야 하는 문제였다.

대학에 들어 가서도 전공 필수를 제외하고 수학과, 물리학과, 전산학과 과목들을 두루 수강했다. 그 중에서 수강한 수학과목이 공업수학(Engineering Mathematics), 선형대수(Linear Algebra), 미분방정식(Differential Equation), 미분기하학(Differential Geometry) 등의 과목들이었고, 더해서 개인적으로는 물리수학(Mathematics for Physics), 복소수 해석(Complex Analysis) 책을 사서 혼자 공부하기도 했다. 그러고 보면 수학 과목을 좋아했던 것은 사실로 보인다.

이러한 중학교, 고등학교, 대학교에서 수학을 통해서 논리력, 사고력, 상상력, 창의력을 키워온 것 같다. 하지만 공학의 전문 영역에 들어온 지난 30년 동안에 이러한 고급 수학을 직접 쓴 경우는 거의 없었다.

매일 매일의 연구에는 아주 간단한 미적분, 벡터, 행렬 곱셈 정도만 쓰인다. 그것도 개념의 설정이 중요하고 융합이 중요하다. 미적분도 sin(x) 의 미분이 cos(x) 라는 정도만 필요하다. 그보다 수학의 개념을 잘 파악하는 것이 중요하다. 복잡하고 어려운 수학은 컴퓨터가 다 풀어 준다. 그래서 점점 수학용 소프트웨어인 MATLAB(수학, 그래픽, 프로그래밍 소프트웨어)이나 컴퓨터와 지내는 시간이 점점 늘어나고 있다.

4차 산업혁명 인공지능에 필요한 수학

4차 산업혁명을 맞아 인공지능이 큰 주제로 등장하고 있다. 인공지능 기술이 가져올 미래 사회의 변화는 상당히 크게 나타날 전망이다. 1차 산업혁명이 노동을 대체한 ‘기계 혁명’ 이라고 한다면, 2차 산업혁명은 전기에너지 기반한 ‘대량생산 혁명’으로 불릴 수 있고, 3차 산업혁명은 인터넷 기초한 ‘정보혁명’ 이라면 4차 산업혁명은 빅데이터를 기반한 ‘인공지능 혁명’으로 생각한다.

그럼 인공지능 알고리즘을 개발하거나 이용하는 개발자 입장에서 필요한 수학은 무엇일까? 아쉽게도 대부분의 인공지능 개발자와 사용자에 필요한 수학은 고등학교 수준의 ‘행렬’ 과 ‘미적분의 개념’ 정도이다. 고등학교 교과서 내용의 개념만 이해해도 된다고 생각한다.

빅데이터 시대의 디지털 데이터 자체가 행렬이다. 영상 이미지 데이터도 그렇고 빅데이터를 저장하는 반도체 메모리도 2차원적인 배열이다. 행렬 곱셈, 덧셈 원리와 절차만 알면 된다. 이 내용은 잘 설명하면 중학생도 이해 할 수 있다. 다양한 신경세포(Node)와 연결층(Layer)을 머리 속에 상상의 연결선 그래프로 그릴 수 있으면 된다. 연결선 그래프를 행렬 수식으로 표현할 수 있으면 된다. 이 과정은 딥러닝 구조의 설계와 학습 과정 설계에서 사용된다.

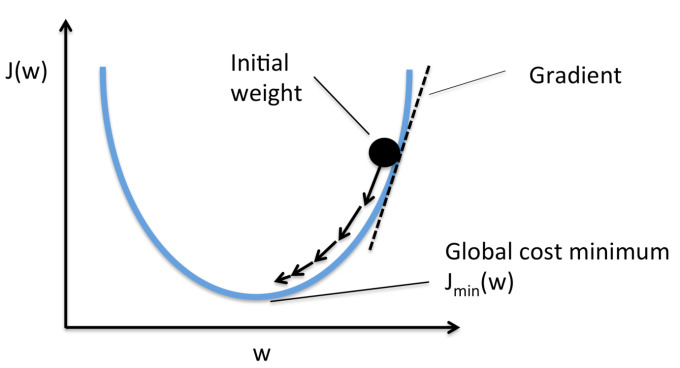
인공지능은 학습을 통해서 지능이 증가하게 된다. 그 학습은 빅데이터를 이용하게 되고, 그래서 데이터가 클수록 인공지능이 똑똑해 진다. 이러한 인공지능의 종류인 지도학습(Supervised Learning)에서는 학습과정에서 데이터를 입력하고 정답을 가르치게 된다. 정답이 틀리고 오차가 생기면 그 오차를 줄이기 위해서 인공지능 연결선의 가중치 값(Weight)들을 고쳐 나가게 된다.

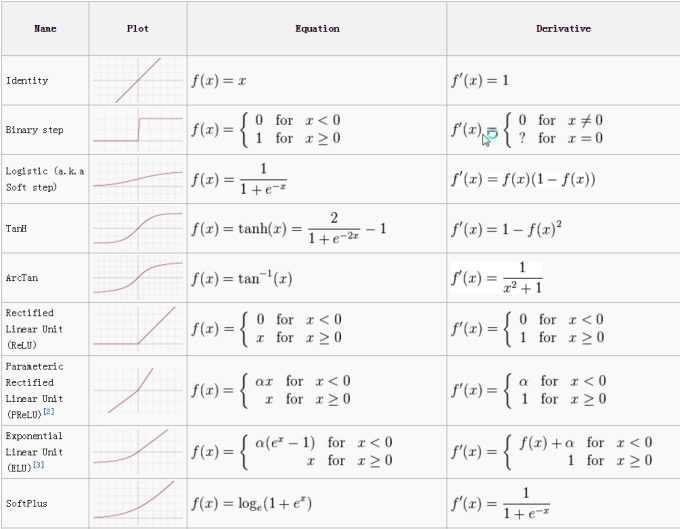
이 과정을 역방향 학습(Back Propagation)이라고 한다. 이때 오차를 최소화 하기 위해서 미분과 함수 기울기의 개념이 들어간다. 신경세포에 들어가는 함수를 활성화 함수(Activation function)라고 하는데 이 함수의 기울기(Gradient) 값이 사용된다. 그런데 이 활성화 함수도 간단한 삼각함수와 지수 함수의 조합으로 이루어져 있다. 그러니 이 활성화 함수의 미분도 고등학교 수학의 범위를 크게 벗어나지 않는다. 인공지능 프로그램을 사용하는 입장에서는 고등학교 수학의 개념만 잘 알아도 된다.

그런데 고급 인공지능 알고리즘에 확률과 통계 고급 수학이 쓰이기도 한다. 인공지능에 모든 경우의 수를 학습하기 어렵기 때문에 확률과 통계의 힘을 필요로 하는 경우가 많기 때문이다. 아예 수학 수식 해를 구하기 보다는 난수(Random Number)를 만들어 내고 이 난수를 이용해서 수학의 답을 구하기도 한다. 세상에는 정확한 수식으로 답을 구할 수 없는 문제가 많기 때문이다. 그래서 인공지능의 기초 혁신에는 확률과 통계가 더 중요한 수학이 된다. 인공지능 수학자가 되려면 대학, 대학원에서 확률과 통계를 전공해도 좋다.

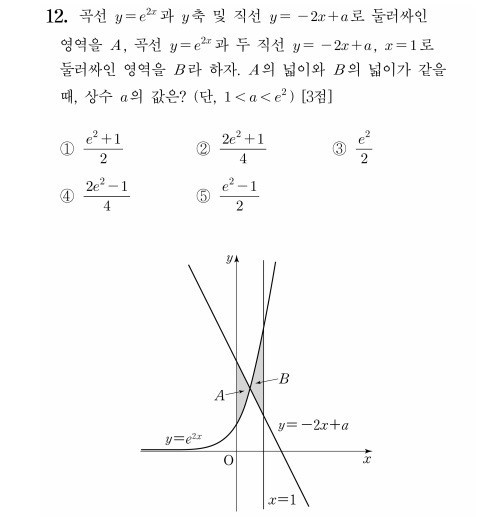
갈 길을 잃은 대입 수능 수학 시험

인공지능을 이용한 프로그램을 짜다가 보면, 개발자는 개념의 설정과 구조의 설계를 하고 실제 수학 문제는 전용 소프트웨어가 풀어준다. 논리적 사고력을 바탕으로 일의 순서를 정하고 그림이나 차트로 표현한다. 그리면 쉽게 컴퓨터 코딩으로 전환 가능하다. 그러니 개념과 절차의 설계, 구조의 설정이 중요하다. 컴퓨터는 복잡한 수학 문제, 많은 영의 수학 계산을 인간보다 휠씬 빠르고 정확하게 푼다. 그러니 양과 속도에서 인간이 경쟁하기 어렵다. 그래서 인간의 생각의 힘이 중요하다.

최근 대학 입학 수능 문제를 보면, 학생의 변별력을 위해서 그리고 입시 공정성을 위해서 빠르게 많은 문제를 푸는 능력이 중요한 것으로 보인다. 이제 4차 산업혁명 시대에는 그것은 컴퓨터가 할 일이다. 현재의 대학 입학 수능 시험 문제 출제 의도는 4차 산업혁명과 인공지능 시대를 역행한다. 지금의 대학 입시 수학 교육과 문제 풀이 방식은 오히려 맑고 밝은 두뇌를 가진 우리 청소년의 창의적인 뇌를 점점 퇴화시키고 있다.

joungho@kaist.ac.kr   

[김정호 카이스트 전기 및 전자공학과 교수]