
10진법의 기원과 응용
우리는 태어나서부터 자연스럽게 '10진법'을 기초로 해서 숫자를 배우고, 산수를 계산한다. 10진법에서는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 이렇게 열 가지를 사용한다. 그리고 초등학교 2~3학년 때 10진법 구구단을 외운다. 10진법과 평생을 같이한다.
이렇게 우리의 계산과 수학이 대부분 10진법을 기반으로 하는 이유는 인간의 손가락이 10개이기 때문이다. 아기에게 숫자를 가르칠 때, 또는 손가락으로 숫자를 표현할 때, 열 개의 손가락으로 표현한다. 아마 우리 인간의 손가락 숫자가 달랐으면 10진법이 사용되지 않았을 것이다. 만약 손가락이 12개였으면 12진법이 주로 사용되었을 것이다.
10진법의 연장으로 대학에서 공학 관련 숫자를 표현할 때, 큰 범위의 숫자를 10의 지수로 표현한다. 예를 들어 10의 3승인 1000의 단위를 킬로(K)로 표시하고, 10의 6승인 백만 단위를 메가(M), 10의 9승인 10억 단위를 기가(G)로 표시한다. K, M, G 단위 모두 10의 지수의 또 다른 표현이다. 이렇게 아주 큰 자연의 숫자를 10이 몇 번 곱한 수인가 하는 기준으로 크기를 표현한다.
빅데이터 시대를 맞아 더 큰 숫자가 필요하게 됐다. 그래서 10의 12승인 테라(Tera) 단위와 10의 15승인 페타(Peta) 단위, 10의 18승인 제타(Zeta) 단위도 쓰이기 시작했다. 빅데이터 시대를 맞자 미래에는 10의 100승 단위도 필요할 전망이다. 이는 공학에서 10의 지수가 유용하게 쓰이는 예이다.
반대로 공학에서 큰 단위를 줄여 간단히 표현하고자 할 때, 로그(log) 함수를 사용한다. 로그 함수를 사용하면 아주 큰 지수 함수를 단순한 대수 숫자로 표현할 수 있다. 그래서 로드 함수를 이용하면 복잡한 곱셈 계산을 간단한 덧셈으로 변환하고, 복잡한 나눗셈 계산을 간단한 뺄셈으로 변환한다.
더 나아가 로그 함수는 복잡한 삼각함수의 주파수와 위상 계산을 간단한 대수 덧셈 뺄셈 계산으로 바꿔주는 편리한 함수이다. 이렇게 로그 함수의 밑수를 10으로 선택하면, log(10의 12승, 테라)=12가 된다. 10의 12승의 큰 숫자를 간단히 12로 표현할 수 있다.
결국 빅데이터인 테라 단위를 12라는 간단한 숫자로 바꾸게 된다. 그 단위를 dB(데시벨)로 표현한다. 그래서 빅데이터도 로그함수에서는 18밖에 되지 않는다. 로그 함수가 빅데이터 시대에 잘 쓰이는 함수이다.

그런데 이와 같은 10진법의 단점도 있다. 또 10진수 지수 함수나 로그 함수의 미적분은 불편하다. 반면에 자연로그 및 자연 상수(e=2.7182818284)를 기초로 지수나 로그 함수를 만들면 미적분이 더욱 간편해진다. 그러면 지수 함수의 미분도 자신의 지수함수가 된다. 공학에서 유용한 성질이다.
다음으로 10진법에서는 10의 약수가 1, 2, 5, 10 이다. 10의 배수는 이들의 약수 조합의 곱으로 표현된다. 여기에 소수는 2와 5이다. 그래서 2와 5의 곱 형태가 된다. 하지만 자연의 중요한 소수인 2와 3이 빠져있다. 그래서 자연수를 완전히 표현하는데 부자연스럽다.
반면에 12의 약수는 1, 2, 3, 4, 6, 12 이고 여기에 포함된 소수가 2, 3이다. 그래서 12진법이 유용한 경우도 있다. 야드파운드법의 피트-인치가 12진법 활용의 대표적 사례이다.
역사적으로도 프랑스 혁명 시기에 도량형을 개선하려고 했지만, 시간만큼은 10진법으로 바꾸지 못했다. 이처럼 진법은 역사, 자연과 인간의 환경을 반영한다.
이러한 장단점에도 불구하고 우리가 실생활에서 대부분 10진법을 주로 사용하는 이유는 우리의 두 손 손가락 개수가 인공지능 시대에도 여전히 10이기 때문이다.
인공지능은 2진법 수학
그런데 인공지능은 손가락이 2개인 지능이다. 그래서 0, 1 두 가지 디지털 숫자만 있는 2진법을 사용한다. 그 이유는 인공지능은 학습에 필요한 데이터 자체가 디지털로 표현되어 있기 때문이다. 데이터를 표현할 때 2진수인 데이터 값은 0과 1로 표현한다. 데이터의 생산자인 센서도 물리 값 자체는 아날로그이지만, 최종 끝에는 디지털 값으로 변환한다.
그래서 센서 출력을 디지털로 표시하고, 저장장치인 메모리에도 0과 1로 표현된다. 센서와 저장장치 사이의 데이터 통신도 그대로 디지털로 한다. 4차 산업혁명 데이터 전체가 디지털로 이루어져 있고, 디지털은 바로 2진수이다.
이렇게 인공지능 계산이 2진수 계산인 것은 그 계산 장치인 실리콘 프로세서와 메모리가 2진수 계산만 할 수 있기 때문이다. 인간처럼 10진수 계산을 하지 못한다. 실리콘 반도체의 스위칭 특성과 메모리가 저장 기능은 0과 1만 생산하고 보관한다. 결국 인공지능은 2진법 세상이다. 인공지능에는 손가락이 디지털 0과 1인 두 가지 상태만 존재하기 때문이다.
여기에 더해 인공지능 알고리즘을 계산하기 위해서는 행렬의 곱셈과 덧셈, 저장이 순차적으로 진행된다. 이 인공지능 계산도 실리콘 프로세서 내에서 2진수 논리 연산의 연속으로 이뤄진다.
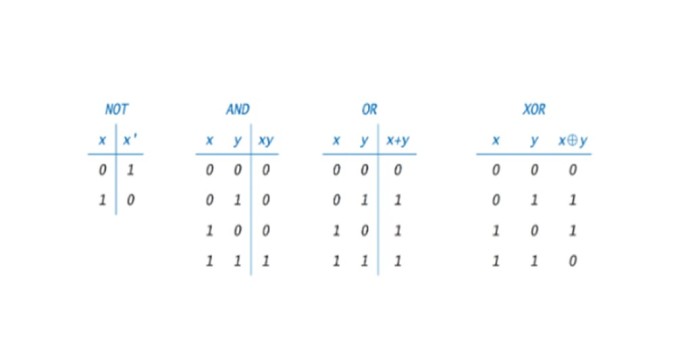
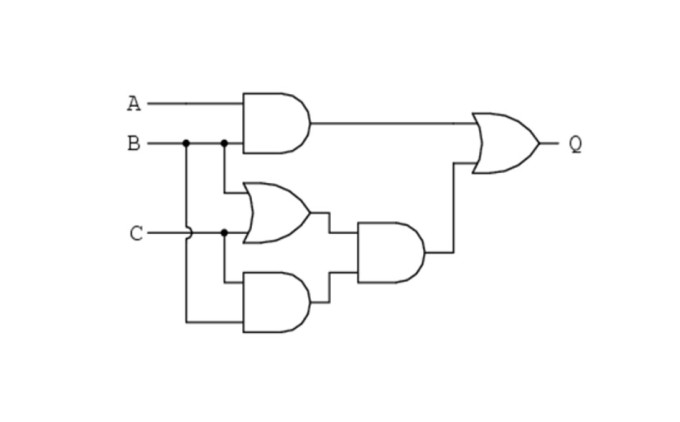
이러한 2진수 연산은 2진수의 논리인 AND, OR, NOT의 조합으로 이뤄진다. 컴퓨터 내에서는 이렇게 2진수의 논리를 실리콘 트랜지스터 회로로 구현하고, 그 묶음으로 곱셈, 덧셈을 한다. 이를 모아서 인공지능 계산 학습과 판단을 한다. 그러니 인공지능은 완전히 2진법 세상이다.
초등학교부터 2진법 산수 필요
인공지능 시대인 미래에는 4가지 직업만 남을 전망이다. 아주 기초적인 육체노동을 하거나, 소프트웨어 코딩을 하거나, 소프트웨어 관리를 하거나, 소프트웨어를 이용한 사업을 운영하는 직업이다.
그러려면 소프트웨어 코딩 능력이 필요하고, 인공지능 알고리즘과 컴퓨터에 대한 이해가 필수적이다. 그런데 코딩, 인공지능, 컴퓨터 모두 2진법으로 운영된다.
따라서 미래에 우리가 직업을 갖기 위해서는 10진법처럼 2진법을 자연스럽게 이해하고 써야 할 수도 있다. 초등학생이 10진법 구구단을 외우듯이, 미래에는 초등학생이 2진법 구구단을 외워야 할 수도 있다.
세상에 고정된 것은 없다. 상상력과 창의력, 유연함이 직업의 경쟁력이 된다. 2진법 세계에서는 손가락이 10개 나오는 장갑보다는 벙어리장갑이 더 어울린다. 잎이 떨어지고 겨울이 다가오기 전에 디지털 장갑이 필요하다.
[김정호 카이스트 전기 및 전자공학과 교수] joungho@kaist.ac.kr























