알고보면 흥미로운 선형대수(linear algebra. 線型代數)

보통 고등학교 때 처음 수학 ‘행렬’을 배운다. 행렬은 다차원적인 숫자의 나열로 2차원인 경우 '(x,y)'로 표현된다. 대부분의 고등학교 수학처럼 왜 배워야 하는지, 어디 쓰는지 그때 알기 어렵다. 그런데 이 행렬 수학이 ‘인공지능 컴퓨터 계산’의 핵심 방법이다.

필자는 대학 2학년때 ‘선형 대수학’이라는 수학과목을 수강했다. 행렬의 수학적 의미와 원리를 배운다. 이 과목은 필자가 대학 때 공부한 과목 중에 가장 감동적이고 재미가 있었다. 수학 논리 전개의 아름다움을 깊이 느끼는 계기가 됐기 때문이다. 전기공학이나, 전자 공학, 전산 과목 또는 물리학 과목이 아니라 ‘수학과목’이었던 기억이 흥미롭고 그 중에서도 선형대수학이라는 과목이라는 점도 지금도 신기하다.

선형대수학에서는 벡터에서 출발해서 행렬의 정의하고 행렬의 기본이 되는 원리들을 순서대로 제시하고 증명한다. 행렬 속의 각 열 벡터가 서로 상호 의존적인가 독립적인가 논의한다. 서로 선형적이면 종속적이고 비선형적이면 독립적이다. 각 열 벡터가 독립적 벡터로 이루어진 행렬은 역행렬이 존재하고 구할 수 있다. 역행렬이 존재하는 행렬은 그 벡터들을 더하고 곱해서 변형하면 대각행렬(Diagonal Matrix, 대각선 부분 숫자만 있고 나머지는 모두 ‘0’인 행렬)가 될 수 있다.

선형대수 과목에서는 이러한 이론들을 처음부터 끝까지 200 여 페이지 책에서 순서대로 빈틈없이 증명한다. 처음부터 끝까지 한 개의 논리적 오점 없이 전체를 증명하고 전개해 간다. 이러한 논리의 완결성이 눈부시기까지 하다. 완벽하게 논리적이다.

강아지와 고양이를 구분하게 해주는 'CNN 알고리즘'

요즈음 행렬 계산이 공학적으로 더욱 중요해 지고 있다. 모든 빅데이터가 디지털로 기록되기 때문이다.

그 중에서도 데이터의 깊이가 크고 정보량이 많은 데이터가 영상 이미지이다. 카메라에서 얻은 이미지는 카메라 센서가 2차원 평면 배열로 되어 있다. 이 배열 자체가 (x,y) 2차원이다. 여기에 색깔 정보, 밝기 정보, 빛의 세기 정보가 더해지면 N 차원 정보가 되고 이를 수학적으로 표시하면 N 차원 행렬이 된다. 그래서 유튜브의 사용이 더욱 확대되면 행렬 계산양도 늘어난다.

인공지능 딥러닝 알고리즘 중에서 영상 이미지 판독에 가장 유효하게 쓰이는 방법이 CNN(Convolution Neural Network) 이라는 알고리즘이다. CNN 에는 여러 개의 신경망 층으로 이루어져 있다. 쉽게 이야기해서 CNN 입력으로 사진이 들어가면 CNN이 강아지인지, 고양이 인지, 곰인지, 사슴인지 찾아 낸다.

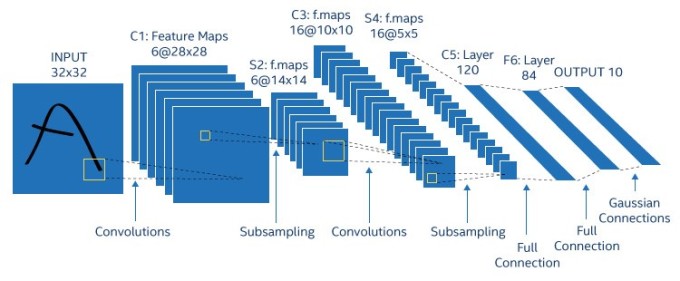
그런데 이 CNN 에서 여러 개의 신경망 층(Layer)을 지나면서 각 층의 출력이 단순화되고 추상화 되어 나간다. 이러한 과정을 거치면서 입력이 수천 다차원 행렬이라 하더라도 최종 출력은 ‘동물의 이름’이 되기 때문이다. 이렇게 크기가 큰 행렬을 줄여나가는 과정을 수학적으로 함수 합성곱(Convolution) 이라고 한다. 이 과정은 수식적으로 볼 때 크기가 큰 행렬에 작은 크기의 행렬을 계속 곱해서 얻는다.

이 곱하는 작은 행렬을 필터 행렬이라고 한다. 이렇게 되면 각 신경망 층이 추상화(Abstraction) 과정을 하게 된다. 첫 층의 입력이 사진이라면 2층은 윤곽을 표현하고, 3층은 코, 입, 귀를 판단하고, 뒷 부분 층은 남녀 인종 등을 파악하고 최종적으로 누구인지 파악하는 과정을 거친다. 이처럼 CNN 에서도 학습과정에서 계속해서 행렬 연산이 이루어져 있다.

행렬과 텐서

그러니 인공지능을 위한 프로그램을 만들기 위해 소프트웨어 코딩을 한다는 것은 수많은 행렬연산을 계획된 순서대로 짜는 것과 같다. 특히 인공지능의 학습과정과 ‘판단(Decision)’ 혹은 ‘추론(Inference)’을 내릴 때 수 많은 행렬 연산을 한다. 그래서 인공지능을 연구하고 개발한다는 의미는 행렬 연산에 묻혀 사는 것과 같다.

이처럼 다차원 행렬을 수학에서 텐서(Tensor)라고 부른다. 그러므로 스칼라(Scalar)는 ‘0 텐서’, 벡터(Vector)는 ‘1 텐서’, 행렬은 ‘2 텐서’라고 부르기도 한다. 구글에서 제공하는 인공지능 계산 플랫폼을 텐서 플로우(Tensor Flow) 라고 부르는 것이 이런 배경이 된다. 인공지능에서 다 차원 행렬인 텐서 계산이 딥러닝 층을 지나가면서 쭉 흘러간다. 이 수학적인 과정이 학습과 판단 과정이다.

재미있는 드라마에는 ‘암시’를 주고 되살아나는 과정이 있으며, 이 과정이 드라마의 재미를 더해 준다. 암시는 장면, 만남, 표정, 대사에서 다양하게 나타난다. 특히 드라마 초반에 나타나 미래 전개 과정을 암시한다. 필자가 대학 2학년 때 선형대수 과목에 푹 빠졌던 것은 40년 후 다가올 4차 산업혁명 시대와 인공지능 시대를 암시했는지도 모른다.

joungho@kaist.ac.kr

[김정호 카이스트 전기 및 전자공학과 교수]